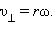Законы Кеплера
- Законы Кеплера
- Первый закон Кеплера (закон эллипсов)
- Второй закон Кеплера (закон площадей)
- Третий закон Кеплера (гармонический закон)
- Ссылки
- Автор
Законы Кеплера
Зако́ны Ке́плера — три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом 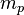 /
/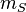 → 0, где
→ 0, где 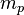 ,
, 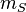 — массы планеты и Солнца.
— массы планеты и Солнца.
Первый закон Кеплера (закон эллипсов)
Все планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце.
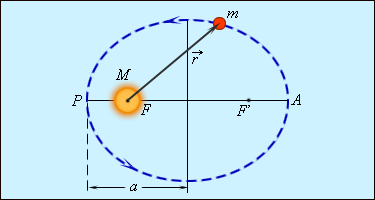
На рис. 1.24.2 показана эллиптическая орбита планеты, масса которой много меньше массы Солнца. Солнце находится в одном из фокусов эллипса. Ближайшая к Солнцу точкаP траектории называется перигелием, точка A, наиболее удаленная от Солнца – афелием. Расстояние между афелием и перигелием – большая ось эллипса.
|
Рисунок 1.24.2.Эллиптическая орбита планеты массой m << M. a – длина большой полуоси, F и F' – фокусы орбиты |
Почти все планеты Солнечной системы (кроме Плутона) движутся по орбитам, близким к круговым.
Второй закон Кеплера (закон площадей)
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
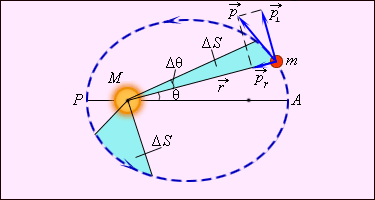
Рис. 1.24.3 иллюстрирует 2-й закон Кеплера.
|
Рисунок 1.24.3.Закон площадей – второй закон Кеплера |
Второй закон Кеплера эквивалентен закону сохранения момента импульса. На рис. 1.24.3 изображен вектор импульса тела 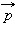 и его составляющие
и его составляющие  и
и 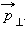 Площадь, заметенная радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:
Площадь, заметенная радиус-вектором за малое время Δt, приближенно равна площади треугольника с основанием rΔθ и высотой r:
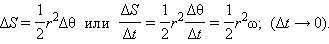 |
Здесь 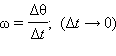 – угловая скорость.
– угловая скорость.
Момент импульса L по абсолютной величине равен произведению модулей векторов 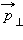 и
и 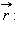
|
Из этих отношений следует:
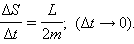 |
Поэтому, если по второму закону Кеплера 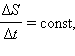 то и момент импульса L при движении остается неизменным.
то и момент импульса L при движении остается неизменным.
В частности, поскольку скорости планеты в перигелии 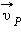 и афелии
и афелии 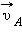 направлены перпендикулярно радиус-векторам
направлены перпендикулярно радиус-векторам 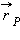 и
и 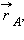 из закона сохранения момента импульса следует:
из закона сохранения момента импульса следует:
| rPυP = rAυA. |
Третий закон Кеплера (гармонический закон)
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит:
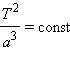 или
или 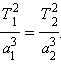
Третий закон Кеплера выполняется для всех планет Солнечной системы с точностью выше 1 %.
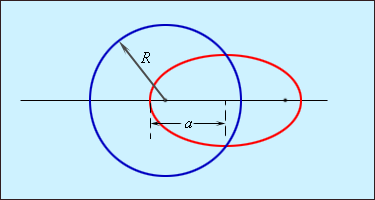
На рис. 1.24.4 изображены две орбиты, одна из которых – круговая с радиусом R, а другая – эллиптическая с большой полуосью a. Третий закон утверждает, что если R = a, то периоды обращения тел по этим орбитам одинаковы.
|
Рисунок 1.24.4.Круговая и эллиптическая орбиты. При R = a периоды обращения тел по этим орбитам одинаковы |
Ссылки
- Википедия - свободная энциклопедия ru.wikipedia.org
Автор
Шкурко В.И.
группа 2-ТМ-55
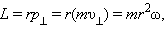 так как
так как