• Поняття математичного маятника
• Положення рiвноваги маятника
• Рiвняння руху
• Малi коливання
• Коливання довільної амплітуди
• Посилання
• Автор

Поняття математичного маятника

Математичний маятник — теоретична модель маятника, в якій матеріальна точка масою m підвішена на невагомому нерозтяжному стержні довжини l і здійснює рух в вертикальній площині під впливом сил тяжіння з прискоренням вільного падіння g.

Модель нехтує розмірами тіла, деформацією підвісу та тертям в точці підвісу стержня. Звичайно розглядаються коливання маятника в одній площині. В загальному випадку, якщо відхилити маятник від положення рівноваги та штовхнути його вбік, рух маятника буде складатися з коливань в вертикальних площинах та руху в горизонтальних.

При малому відхилені математичний маятник здійснює гармонічні коливання. Якщо відхилення велике, то коливання маятника періодичні, але не гармонічні.

Положення рiвноваги маятника

Математичний маятник має два положення рівноваги: стійке та нестійке.

В стійкому положенні рівноваги маятник висить непорушно строго вертикально, сила тяжіння врівноважується силою пружності стержня. Якщо відвести маятник від положення рівноваги, або надати йому початкової швидкості, виникають коливаня. Сили тертя, що діють на реальний маятник але не враховані в даній моделі, приводять до загасання коливань та знов повертають маятник в початкове положення. Саме тому це положення має назву стійкого.

Інше положення рівноваги математичного маятника знаходиться в точці , тобто коли стержень орієнтований вертикально вгору. В цьому положенні сили тяжіння та пружності стержня, як і в точці стійкої рівноваги, зрівноважені, проте дана рівновага є нестійкою. При найменшому відхиленні від вертикального положення рівнодійна сил, що діють на маятник, виводить його з рівноваги. Реальний маятник вже ніколи не повернеться в це положення. Підтримати маятник у вертикальному положенні можна за допомогою балансування, яке зводиться до особливих рухів точки опори.
[ред.]

Рiвняння руху

Найлегше вивести рівняння руху математичного маятника, скориставшись рівннями Лагранжа. Їх можна також вивести, розглядаючи сили, які діють на тягарець, і записуючи для цих сил другий закон Ньютона.

Нехай маятник відхилився від положення рівноваги на кут θ між вертикаллю й стержнем (див. малюнок).

Потенціальна енергія математичного маятника дорівнює
,

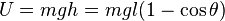
де h- висота відносно найнижчого положення.

Кінетична енергія в будь-який момент часу t визначається моментом інерції I та кутовою швидкістю ω:
.
Момент інерції матеріальної точки масою m відносно осі, яка проходить перпендикулярно до площини рисунка через точку підвісу, дорівнює
.
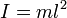
Функція Лагранжа математичного маятника для узагальненої координати θ дорівнює
.
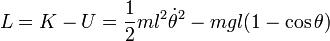
Рівняння Лагранжа

визначає рівняння руху маятника
.

Малi коливання

При малих коливаннях і рівняння руху маятника зводиться до рівняння гармонічного осцилятора

,

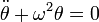
де частота власних коливань математичного маятника
.

При малих коливаннях відхилення маятника від положення рівноваги описується формулою
,

де амплітуда коливань та фаза визначаються початковими умовами, тобто тим наскільки маятник відхилили від положення рівноваги, як сильно його штовхнули тощо.
[ред.]

Коливання довільної амплітуди

У випадку, коли початкове відхилення, або початкова швидкість не малі, коливання математичного маятника залишаються строго періодичними, але не є синусоїдальними, тобто стають ангармонічними. Загальний розв'язок рівняння руху математичного маятника має вигляд:
,

де , позначення 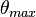 означає максимальне відхилення від положення рівноваги, sn( x ) - еліптичний синус.

Період коливань математичного маятника залежить від амплітуди, тобто від початкового відхилення. Але навіть при відхиленні на 60° відхилення частоти від формули, наведеної для малих коливань, не перевищує 15%.

Посилання

1. Википедия - свободная энциклопедия ru.wikipedia.org
2. Федорченко А.М. Теоретична механіка.

Автор

Трасковський Ю.В. 2-ТМ-55