Закон всемирного тяготения
Редактировал(а) Dmitry Fedin 2018/10/19 11:41
Формулировка
Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.
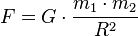
Здесь r − расстояние между центрами масс данных тел, G − гравитационная постоянная, значение которой, найденное экспериментальным путем, составляет 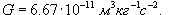 .
.
Свойства ньютоновского тяготения
- В ньютоновской теории каждое массивное тело порождает силовое поле притяжения к этому телу, которое называется гравитационным полем. Это поле потенциально, и функция гравитационного потенциала для материальной точки с массой
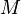 определяется формулой:
определяется формулой:
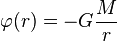
- В общем случае, когда плотность вещества ρ распределена произвольно, φ удовлетворяет уравнению Пуассона:

- Решение этого уравнения записывается в виде:
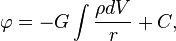
- где r — расстояние между элементом объёма dV и точкой, в которой определяется потенциал φ, С — произвольная постоянная.
- Сила притяжения, действующая в гравитационном поле на материальную точку с массой
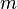 , связана с потенциалом формулой:
, связана с потенциалом формулой:
- Сферически симметричное тело создаёт за своими пределами такое же поле, как материальная точка той же массы, расположенная в центре тела.
- Траектория материальной точки в гравитационном поле, создаваемом много большей по массе материальной точкой, подчиняется законам Кеплера. В частности, планеты и кометы в Солнечной системе движутся по эллипсам или гиперболам. Влияние других планет, искажающее эту картину, можно учесть с помощью теории возмущений.
Ссылки
- Википедия - свободная энциклопедия ru.wikipedia.org
Автор
Мищенко М. 2-ТМ-55
