Кинематика твёрдого тела
- Аддитивность угловой скорости
- Дифференцирование по времени
- Формула Эйлера
- Ускорение Кориолиса
- Ссылки
- Автор
Кинема́тика твёрдого тела (от др.-греч. κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.
Аддитивность угловой скорости
Если тело вращается с угловой скоростью 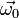 в системе отсчёта
в системе отсчёта  , а эта система отсчёта, в свою очередь, вращается относительно системы отсчёта
, а эта система отсчёта, в свою очередь, вращается относительно системы отсчёта 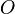 с угловой скоростью
с угловой скоростью  , то это тело вращается относительно
, то это тело вращается относительно 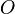 с угловой скоростью
с угловой скоростью
Дифференцирование по времени
Вращающееся тело — неинерциональная система отсчёта. Поэтому оператор дифференцирования по времени для векторов, определённых в покоящейся системе координат 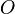 , связан с оператором дифференцирования по времени для векторов, определённых в системе координат на вращающемся теле
, связан с оператором дифференцирования по времени для векторов, определённых в системе координат на вращающемся теле  , соотношением:
, соотношением:
 ,
,
где « » — векторное произведение.
» — векторное произведение.
Формула Эйлера
Формула Эйлера связывает скорости двух точек твёрдого тела:
 ,
,
где 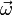 — вектор угловой скорости тела.
— вектор угловой скорости тела.
Выводится эта формула путём дифференцирования формулы  по времени с учётом замены оператора для неинерциональной системы отсчёта (см. выше). Путём повторного дифференцирования можно получить связь ускорений двух точек:
по времени с учётом замены оператора для неинерциональной системы отсчёта (см. выше). Путём повторного дифференцирования можно получить связь ускорений двух точек:
 ,
,
где 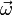 — вектор угловой скорости тела, а
— вектор угловой скорости тела, а 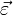 — вектор углового ускорония тела.
— вектор углового ускорония тела.
Второе слагаемое называется центростремительным ускорением.
Ускорение Кориолиса
Ускорение точки B (в покоящейся системе координат), движущейся по поверхности вращающегося тела равно
где  - радиус-вектор точки В в системе координат на вращающемся теле. Последнее слагаемое и будет кориолисовым ускорением.
- радиус-вектор точки В в системе координат на вращающемся теле. Последнее слагаемое и будет кориолисовым ускорением.
Ссылки
- Википедия - свободная энциклопедия ru.wikipedia.org.
Автор
Взоров О.Ю
гр:2-ТМ-55
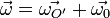
![\vec a=\vec {a}_B + \left[ \vec \varepsilon \times \vec r_B \right] + \left[ \vec \omega \times \left[ \vec \omega \times \vec r_B \right] \right] + 2\left[ \vec \omega \times \vec {v}_B \right],](http://upload.wikimedia.org/wikipedia/ru/math/a/a/7/aa7934ec1b0b8f51e3a6619385828f44.png)